由 ⅛Rl>
Bi Bl Bi Bl
事故树分析法
事故树(Fault Tree Analysis, FTA)也称故障树,是一种描述事故因果关系的 有向逻辑“树”,是安全系统工程中重要的分析方法之一。该法尤其适用于对工 艺设备系统进行危险识别和评价,既适用于定性分析,又能进行定量分析。具有 简明、形象化的特点,体现了以系统工程方法研究安全问题的系统性、准确性和 预测性。FTA作为安全分析评价、事故预测的一种先进的科学方法,已得到国内 外的公认和广泛采用。
1962年,美国贝尔电话实验室的维森(WatSOn)提出此法。该法最早用于 民兵式导弹发射控制系统的可靠性研究,从而为解决导弹系统偶然事件的预测问 题作出了贡献。随之波音公司的科研人员进一步发展了 FTA方法,使之在航空 航天工业方面得到应用。20世纪60年代期,FTA由航空航天工业发展到以原子 能工业为中心的其他产业部门。1974年美国原子能委员会发表了关于核电站灾 害性危险性评价报告(拉斯姆逊报告),对FTA作了大量和有效的应用,引起了 全世界广泛的关注。目前此法已在国内外许多工业部门得到运用。
从1978年起,我国开始了 FTA的研究和运用工作。FTA不仅能分析出事故 的直接原因,而且能深入提示事故的潜在原因,因此在工程或设备的设计阶段、 在事故查询或编制新的操作方法时,都可以使用FTA对它们的安全性作出评价。 实践证明FTA适合我国国情,适合普遍推广使用。
事故树分析是对既定的生产系统或作业中可能出现的事故条件及可能导致 的灾害后果,按工艺流程、先后次序和因果关系绘成程序方框图,表示导致灾害、 伤害事故(不希望事件)的各种因素之间的逻辑关系。它由输入符号或关系符号 组成,用以分析系统的安全问题或系统的运行功能问题,并为判明灾害、伤害的 发生途径及与灾害、伤害之间的关系提供一种最为形象、简洁的表达形式。
事故树分析的基本程序如下:
1) 熟悉系统。要详细了解系统状态、工艺过程及各种参数,以及作业情况、 环境状况等,绘出工艺流程图及布置图。
2) 调查事故。广泛收集同类系统的事故安全,进行事故统计(包括未遂事 故),设想给定系统可能要发生的事故。
.
3) 确定顶上事件。要分析的对象事件即为顶上事件。对所调查的事故进行 全面分析,分析其损失大小和发生的频率,从中找出后果严重且较易发生的事故 作为顶上事件。
4) 确定目标值。根据经验教训和事故案例,经统计分析后,求出事故发生 的概率(频率),作为要控制的事故目标值,计算事故的损失率,采取措施,使 之达到可以接受的安全指标。
5) 调查原因事件。全面分析、调查与事故有关的所有原因事件和各种因素, 如设备、设施、人为失误、安全管理、环境等。
6) 画出事故树。从顶上事件起,按演绎分析的方法,逐级找出直接原因事 件,到所要分析的深度,按其逻辑关系,用逻辑门将上下层连结,画出事故树。
7) 定性分析。按事故树结构运用布尔代数,进行简化,求出最小割(径) 集,确定各基本事件的结构重要度。
8) 求出顶上事件发生概率。确定所有原因发生概率,标在事故树上,并进 而求出顶上事件(事故)发生概率。
9) 进行比较。将求出的概率与统计所得概率进行比较,如不符,则返回5) 查找原因事件是否有误或遗漏,逻辑关系是否正确,基本原因事件的概率是否合 适等。
10) 定量分析。分析研究事故发生概率以及如何才能降低事故概率,并选出 最优方案。通过重要度分析,确定突破口,可行性强的加强控制,防止事故的发 生。
原则上是上述10个步骤,在分析时可视具体问题灵活掌握,如果事故树规 模很大,可借助计算机进行。目前我国FTA 一般都考虑到第7步进行定性分析 为止,也能取得较好效果。
I
事故树是由各种符号与它们相连结的逻辑门所组成。
事故树使用布尔逻辑门(如:“与”,"或“)产生系统的故障逻辑模型来 描述设备故障和人为失误是如何组合导致顶上事件的。许多事故树模型可通过分 析一个较大的工艺过程得到,实际的模型数目取决于危险分析人员选定的顶上事 件数,一个顶上事件对应着一个事故模型。事故树分析人员常对每个事故树逻辑 模型求解产生故障序列,称为最小割集,由此可导出顶上事件。这些最小割集序 列可以通过每个割集中的故障数目和类型定性的排序。一般的,含有较少故障数 目的割集比含有较多故障数目的割集更可能导致顶上事件。最小割集序列揭示了 系统设计、操作的缺陷,对此分析人员应提出可能提高过程安全性的途径。
进行FTA,需要详细了解系统功能、详细的工艺图和操作程序以及各种故障 模式和它们的结果,因此,良好技术素质和经验是分析人员有效和高质量运用 FTA的保证。
1)事故树的符号及其意义:

由 ⅛Rl>
Bi Bl Bi Bl
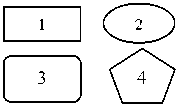
(1) 事件符号:
顶上事件、中间事件符号,需要进一步往下分析的事件;
(
基本事件符号,不能再往下分析的事件; 正常事件符号,正常情况下存在的事件; 省略事件,不能或不需要向下分析的事件。
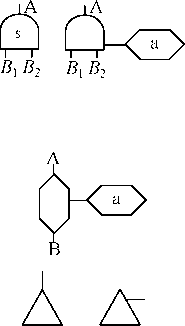
(2) 逻辑门符号:
或门,表示B1和B2任一事件单独发生(输入)时,A 事件都可以发生(输出)。条件或门,表示B1或B2任一 事件单独发生(输入)时,还必须满足条件a,A事件 才发生(输出)。
与门,表示B1和B2同时发生(输入)时,A事件才发 生(输出)。条件与门,表示B1或B2两事件同时发生(输 入)时,还必须满足条件a,A事件才发生(输出)。 限制门,表示B事件发生(输入)且满足条件a时,A 事件才发生(输出)。
转入符号,表示在别处的部分树,由该处转入(在三角 形内标出从何处转入)。转出符号,表示这部分树由该 处转移至他处,由该处转出(三角形内标出向何处转 移)。
2) 布尔代数主要运算法则
由元素a、b、C……组成的集合B,若在B中定义了两个二元运算“+”与 “ •”,则有
(1) 结合律:
?
(a + b) + C = a + (b + C)
(a ∙ b)∙ C = a ∙(b ∙ C)
(2) 交换律:
a + b = b + a a ∙ b = b ∙ a
(3) 分配律:
a ∙ (b + C) = (a ∙ b)+ (a ∙ C)
a + (b ∙ C )= (a + b )∙(a + C)
(4) 在B中存在两个元素0与1,则有:
a + 0 = 0 + a = a
*
a ∙1 = 1 ∙ a = a
(5) 互补律:对于B中每个元素饱存在一个相应的元素a',使得:
a+a - 1
a ∙ ar = 0
(6) 加法等幂律:
a + a = a
(7) 乘法等幂律:
a ∙ a = a
(8) 吸收律:对于B中的任意元素a, b有:
a + ab = a
。
a(a + b) = a
(9) 德•摩尔根律:对于B中的任意元素a, b有:
八'
(a + b) = a b
(ab) = a' + b'
3) 事故树的数字表达式
事故树按其事件的逻辑关系,自上(顶上事件开始)而下逐级运用布尔代数 展开,进一步进行整理、化简,以便于进行定性、定量分析。
例如,有事故树如图1-2所示。
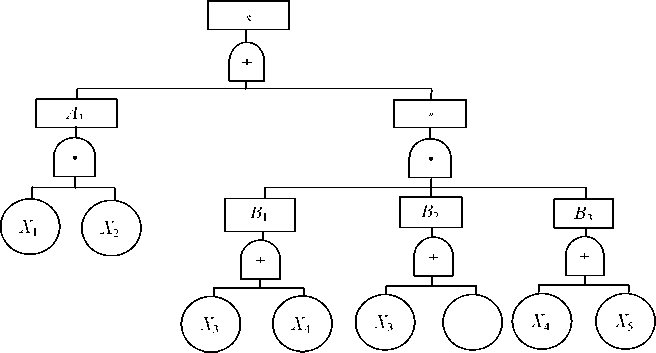
图1-2未经化简的事故树
图示未经化简的事故树,运用布尔代数其结构函数表达式为:
T=A ]+A2=A 1+B1B2B 3
=X1X2+(X3+X4)(X? +XQ(X4+X5) =X1X2+X3X3X4+X3X4X4+X3X4X5+X4X4X5 +X4X5X5+X3X3X5 +X3X5
X5 +X3X4X5
在事故树中,一组基本事件能造成顶上事件发生,则该组基本事件的集合称 为割集。能够引起顶上事件发生的最低限度的基本事件的集合称为最小割集,即 如果割集中任一基本事件不发生,顶上事件就绝不发生。为有效地、针对性控制 顶上事件的发生,最小割集在FTA中有着重要的作用。因此,最小割集的求解 很关键。其求法包括:行列法;结构法;质数代入法;矩阵法;布尔代数化简法 等等。其中,布尔代数化简法比较简单,但国际上普遍承认行列法。
?
1)行列法求解
行列法又称福塞尔法,是1972年福塞尔(FUSSeIl)提出的。
这种方法的原理是从顶上事件开始,按逻辑门顺序用下面的输入事件代替上 面的输出事件,逐层代替,直到所有基本事件都代完为止。在代替过程中,“或 门”连接的输入事件纵向列出,“与门”连接的输入事件横向列出。这样会得到 若干行基本事件的交集,再用布尔代数化简,就得到最小割集。
下面以图所示的事故树为例,求最小割集。
TfAB
X1B
-
CB
X1B
XX3
C X1X3
X1X4
X2X3X3
XLX3
X1X4
LXX3
(2) 从顶上事件T开始,第一层逻辑门为“与门”,“与门”连接的两个事 件横向排列代替T;
(3) A下面的逻辑门为“或门”,连接Xi,C两个事件,应纵向排列,变成 XIB和CB两行;
(4) C下面的“与门”连接X2, X3两个事件,因此X2, X3写在同一行上代 替C,此时得到二个交集X1B,X2X3B。同理将事件B用下面的输入事件代入, 得到四个交集,经化简得三个最小割集。这三个最小割集是:
K1{X 1,X3}; K2{ X2, X3}; K 3(X 1,X4};
化简后的事故树,其结构如图1-4所示,它是图1-3的等效树。
由图可见用最小割集表示的事故树,共有两层逻辑门,第一层为或门,第二 层为与门。由事故树的等效树可清楚看出事故发生的各种模式。
K1
X1 X3 X2 X3 X1 X4
X1
X2
X3
X1 X4
图1-3事故树图
图1-4上图事故树的等效树
2) 布尔代数化简法求解
对比较简单的事故树可用此法求取,它主要利用布尔代数的几个运算定律。 在一个系统中,不安全事件就是安全事件的补事件,不安全事件发生概率用P(S) 表示,安全事件发生概率用P(s')表示,则P(s)+ P(s')=1
布尔代数法求最小割集的步聚是:
首先列出事故树的布尔表达式,即从事故树的第一层输入事件开始,“或门” 的输入事件用逻辑加表示,“与门”的输入事件且逻辑积表示。再用第二层输入 事件代替第一层,第三层输入事件代替第二层,直到事故树全体基本事件都代完 为止,将布尔表达式整理后得到若干个交集的并集,每一个交集就是一个割集, 再利用布尔代数运算定律化简,就可以求出最小割集。
所谓并集就是把两个集合A和B的元素合并在一起。如果合并后的元素构 成的集合叫&则S是A与B的并集,记为S=A ∪B或S=A+Bo
事故树中,或门的输出事件就是所有输入事件的并集。
若两个集合A和B有公共元素,则公共元素构成的集合P称为A与B的交 集,记为P=AnBO
事故树中,与门的输出事件就是其输入事件的交集。
以图事故树为例,求最小割集:
T=AB = (X1+C) (X3+X4 )
^
=(X1+X2X3) (X3+X4)
=X1X3+X2X3X3+XI x4+x2x3x4
=X1X3+X2X3+X1X4
事故树经布尔代数化简后得3个交集的并集,亦即此事故树有3个最小割集:
K1{X 1,X3},K2( X2, X3},K3{X1,X4}0
3) 最小割集的作用
最小割集表示系统的危险性,每个最小割集都是顶上事件发生的一种可能渠 道,最小割集的数目越多,越危险。
其作用如下:
(1) 表示顶上事件发生的原因。事故发生必然是某个最小割集中几个事件同 时存在的结果。求出事故树全部最小割集,就可掌握事故发生的各种可能,对掌 握事故的规律,查明事故的原因提供帮助。
(2) 一个最小割集代表一种事故模式。根据最小割集,可以发现系统中最薄 弱的环节,直观判断出哪种模式最危险,哪些次之,以及如何采取预防措施。
(3) ?
(4) 可以用最小割集判断基本事件的结构重要度,计算顶上事件概率。
(5) 由于一个基本事件发生的概率比两个基本事件同时发生的概率要大得 多,比三个基本事件的同时发生概率更大,故最小割集含有的基本事件越少,发 生顶上事件就越有可能,亦即故障模式危险性大。只有一个基本事件的割集最危 险。
1) 最小径集的概念
与割集相反,在事故树中。有一组基本事件不发生,顶上事件就不会发生, 这一组基本事件的集合叫径集。径集是表示系统不发生顶上事件而正常运行的模 式。同样在径集中也存在相互包含和重复事件的情况,去掉这些事件的径集叫最 小径集。亦即,凡是不能导致顶上事件发生的最低限度的基本事件的集合叫最小 径集。在最小径集中,任意去掉一个事件也不成其为径集。事故树有一个最小径 集,顶上事件不发生的可能性就有一种。最小径集越多,顶上事件不发生的途径 就越多,系统也就越安全。
2) 最小径集的求法
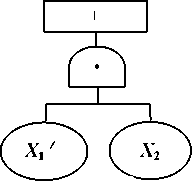
最小径集的求法是利用最小径集与最小割集的对偶性,首先画事故树的对偶 树,即成功树。求成功树的最小割集,就是原事故树的最小径集。成功树的画法 是将事故树的“与门”全部换成“或门”、“或门”全部换成“与门”,并把全部 事件的发生变成不发生,就是在所有事件上都加“'”,使之变成原事件补的形 式。经过这样变换后得到的树形就是原事故树的成功树。(见图1-5)
(a)
(b)
图1-5事故树变成功树示例
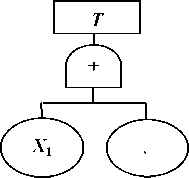
这种做法是根据布尔代数的德•摩根定律。如图所示事故树,其表达式为:
T=X 1+X2
/
该式表示事件X1、X2任一个发生,顶上事件T就会发生。要使顶上事件不 发生,X1、X2两个事件必须都不发生。那么,在上式两端取补,得到下式
T=(X 1+X2)' = X1X2,
该式用图形表示就是图。b是a的成功树。由图可见,图中所有事件都变化, 逻辑门也由“或门”转换成“与门”。
同理可知,画成功树的事故树的“与门”要变成“或门”,事件也都要变为 原事件补的形式,
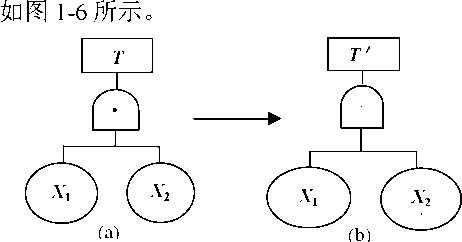
图1-6成功树变事故树示例
“条件与门”、“条件或门”、“限制门”的变换方式同上,变换时,把条件作 为基本事件处理。
下面仍以图1-3事故树为例求最小径集。首先画出事故树的对偶树一一成功 树(如图1-7所示),求成功树的最小上割集。
T =A +B,=X1 Z C + X3' X4 Z
=X1 ' (X2 ' +X3 ' )+X3 ' X4 '
=X I' X2' +X1' X3' +X3' X4 '
;
成功树有三个最小割集,就是事故树的三个最小径集:
P1 = {X1,X2},P 2={X1,X3},P3={X3, X以}
用最小径集表示的事故树结构式为:
T= (X1+X2)(X1 +X5) (X3+X4)
同样,用最小径集也可画事故树的等效树,用最小径集画图1-5事故树的等 效树结果如图1-8所示。
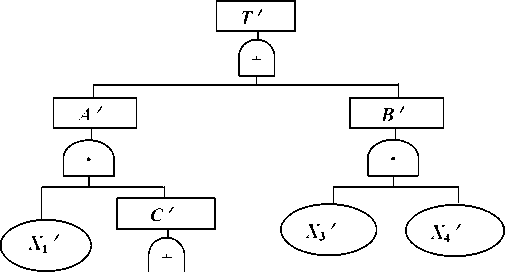
图1-7事故树变成功树示例
用最小径集表示的等效树也有两层逻辑门,与用最小割集表示的等效树比 较,所不同的是两层逻辑门符合正好相反。
3)最小径集的作用
最小径集与最小割集在事故树中有着重要的作用:
① 最小径集表示系统的安全性,如事故树中有一个最小径集,则顶上事件不 发生的可能性就有一种;最小径集越多,控制顶上事件不发生的方案就越多,系 统的安全性就越大。
② 由最小径集可选择控制事故的最佳方案,如一个事故树中有几个最小径 集,那么使顶上事件不发生的方案就有几个。一般,控制最小径集中的基本事件 少时比控制最小径集中的基本事件多时,更省工、省时、经济、有效。当然,如 果由于经济和技术上的原因,难以控制,则又当别论,此时应选择其他方案。
$
③ 利用最小径集(或最小割集)可进行结构重要度分析。
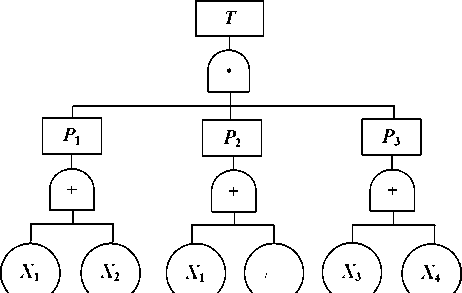
图1-8事故树的等效树
I
1) 结构重要度概念
结构重要度分析,就是不考虑基本事件发生的概率是多少,仅从事故树结构 上分析各基本事件的发生对顶上事件的影响程度。
事故树是由众多基本事件构成的,这些基本事件对顶上事件均产生影响,但 影响程度是不同的,在制定安全防范措施时必须有个先后次序,轻重缓急,以便 使系统达到经济、有效、安全的目的。结构重要度分析虽然是一种定性分析方法, 但在目前缺乏定量分析数据的情况下,这种分析显得很重要。
结构重要度分析方法归纳起来有两种,第一种是计算出各基本事件的结构重 要系数,将系数由大到小排列得各基本事件的重要顺序;第二种是用最小割集和 最小径集近似判断各基本事件的结构重要系数的大小,并排列次序。
2) 结构重要系数求取
下面介绍结构重要系数的求取方法。假设某事故树有几个基本事件,每个基 本事件X的状态都有两种:
Y = J 0表示基本事件状态不发生;
=L 1表示基本事件状态发生
已知顶上事件是基本事件的状态函数,顶上事件的状态用©表示,即S(X)= Φ(X1,X2,X3, -Xn),则φ(χ)也有两种状态: "
川X)=J 1表示顶上事件状态发生;
例)=L 0表示顶上事件状态不发生
φ(x)叫做事故树的结构函数。
在其他基本事件状态都不变的情况下,基本事件Xi的状态从0变到1,顶上 事件的状态变化有以下三种情况:
(1) 由 φ(0i,X)=0→ φ(1i, x)=0,则有 φ(11, x)- φ(0„ x)=0,即不管基本事件 是否发生,顶上事件都不发生;
(2) 由 Φ(01 ,x)=0→ Φ(11, x)=1,则有 Φ(11, x)-Φ(0i, x)=1,即顶上事件状态 随基本事件状态的变化而变化;
(3) 由 Φ(01, x)=1→ Φ(11, x)=1,则有 Φ(11, x)- Φ(0i, x)=0,即不管基本事件 是否发生,顶上事件也都不发生。
上述三种情况,只有第二种情况是基本事件发生Xi发生,顶上事件也发生。 这说明Xi事件对事故发生起着重要作用,这种情况越多,Xi的重要性就越大。
对由n个基本事件构成的事故树,n个基本事件两种状态的组合数为2n个。 把其中一个事件Xi作为变化对象(从0变到1),其他基本事件的状态保持不变 的对照组共有2n”个。在这些对照组中属于第二种情况[Φ(L,X)- Φ(0i,x)=1] 所占的比例即是Xi事件的结构重要系数,用ls(i)表示。可以用下式求得:
Iφ(i) = 21-1 ∑ [φ(1i, x) -Φ(O i, x)]
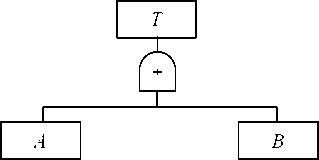
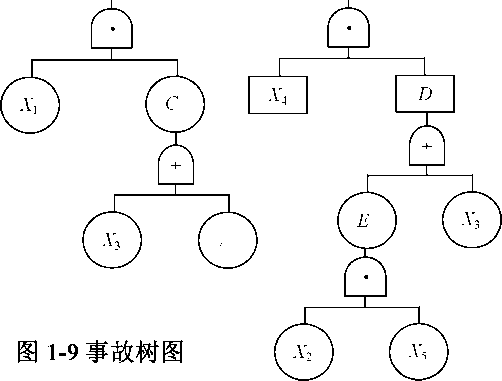
下面以图1-9所示的事故树 为例,说明各基本事件结构重要 系数的求法。
此事故树有5个基本事件, 按照二进制列出所有基本事件 两种状态的组合数,共有25=32 个,这些组合列于表1-7。为便 于对照,将32组分左右两部分 各占16组,然后根据事故树图 或最小割集确定Φ(01, x)和Φ(L, x)的值,以0和1两种状态表示。
由表可见,Xi在左半部的状 态值都为0,右半部都为1,右 半部和左半部对应找出Φ(1, x)-Φ(01, X)= 1的组合,共有7个, 因此,基本事件X1的结构重要 度系数为:
表1-7基本事件状态值与顶上事件状态值
|
X1 |
X2 |
X3 |
X4 |
X5 |
Φ(O1, x) |
X1 |
X2 |
X3 |
X4 |
X5 |
Φ ( 1 1,x) |
|
0 |
0 |
0 |
0 |
0 |
[ 0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
I 0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
* 0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
Y 0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
\ 1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
。 0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
? 0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
# 1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
< 0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
! 1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
( 0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
# 1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
】 0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
(- 1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
( 1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
' 1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
】 0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
… 1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
〜 1_____________ |
1 |
1 |
1 |
1 |
1 |
1 |
基本事件X2在表1-7中左右两侧,其状态值都分成上下两部分,每部分8
组,在同一侧上下部分对照找出Φ(12, x)-Φ(02,x)=1的组合,只有1个,故有 Iφ(2)=1/16
同理可得出
Iφ (3) =7/16
Iφ (4) =5/16
Iφ (5) =5/16
按各基本事件I(1)值的大小排列起来,其结果为:
Iφ (1)= Iφ (3)>Iφ (4)= Iφ (5)>Iφ (2)
用计算基本事件结构重要系数的方法进行结构重要度分析,其结果较为精 确,但很繁琐。特别当事故树比较庞大、基本事件个数比较多时,要排列为2n 个组合是很困难的,有时即使是使用计算机也难以进行。
3)结构重要度分析
结构重要度分析的另一种方法是用最小割集或最小径集近似判断各基本事 件的结构重要系数。这种方法的精确度虽然比采用求结构重要系数法要差一些, 但操作简便,所以应用较多。用最小割集或最小径集近似判断结构重要系数的方 法也有几种,这里只介绍其中的一种:
① 单事件最小割(径)集中基本事件结构重要系数最大。
例如,某事故树有3个最小径集:
(
P1 = {X/},P 2={X2, X3},P 3={X4, X5,X6}
第一个最小径集只含一个基本事件X”按此原则X1的结构重要系数最大。
Iφ(1)>Iφ(i) 7=2,3,4,5
② 仅出现在同一个最小割(径)集中的所有基本事件结构重要系数相等。
例如,上述事故树X2, X3只出现在第二个最小径集,在其他最小径集中都 未出现,所以 I"2)=I"3),同理有 Iφ(4)=Iφ(5)=Iφ(6)。
③ 仅出现在基本事件个数相等的若干个最小割(径)集中的各基本事件结构 重要系数依出现次数而定,即出现次数少,其结构重要系数小;出现次数多,其 结构重要系数大;出现次数相等,其结构重要系数相等。
例如,某事故树有3个最小割集:
Ki ={Xι, X2, X3}, K2 ={Xι, X3, X4}, K3 ={Xι, X4,X5};
此事故树有5个基本事件,都出现在含有3个基本事件的最小割集中。X1 出现3次,X3, X4出现2次,X2,X5只出现1次,按此原则
Iφ(1)>Iφ(3)= Iφ(4)> Iφ(5)= Iφ(2)
Y
④ 两个基本事件出现在基本事件个数不等的若干个最小割(径)集中,其结 构重要系数依下列情况而定:
A. 若它们在各最小割(径)集中重复出现的次数相等,则在少数事件最小割 (径)集中出现的基本事件结构重要系数大。
例如,某事故树有4个最小割集:
Kι={Xι, X3}, K2={Xi, X4},K3={X2, X4, X5},K4={X2, X5, x&}
X1,X2 2个基本事件都出现2次,但X1所在的2个最小割集都含有2个基 本事件,而X2所在的2个最小割集都含有3个基本事件,所以Iφ(1)>Iφ(2)°
B. 若它们在少事件最小割(径)集中出现次数少,在多事件最小割(径)集 中出现次数多,以及其他更为复杂的情况,可用下列近似判别式计算:
∑ I (7) =∑ 2⅛Γ
式中I(Z)——基本事件Xl结构重要系数的近似判别值,Iφ(i)大则I(7)也大;
Xi∈Kj 其中事件Xi属于Kj最小割(径)集;
n——基本事件Xi所在最小割(径)集中包含基本事件的个数。 【
假设某事件树共有5个最小径集:
P1={X1, X3},P2={X1,X4},P3=(X2, X4, X5},P4={X2, X5, X6},P5={X2,
X6, X7}
基本事件Xi与X2比较,Xi出现2次,但所在的2个最小径集都含有2个基 本事件;X2出现3次,所在的3个最小径集都含有3个基本事件,根据这个原则 判断:
111 --1---1-- 23-1 23-1 23-1
由此可知Iφ(1)>Iφ(2)°
利用上述四条原则判断基本事件结构重要系数大小时,必须从第一至第四条 按顺序进行,不能单纯使用近似判别式,否则会得到错误的结果。
用最小割集或最小径集判断基本事件结构重要顺序其结果应该是一样的,选 用哪一种要视具体情况而定。一般来说,最小割集和最小径集哪一种数量少就选 哪一种,这样对包含的基本事件容易比较。例如,图事故树含4个最小割集:
K1={X1, X3},K2={X1, X5},K3={X3, X4},K4={X2, X4, X5}
3个最小径集:
\
P1 = {X1, X4},P 2={X1, X2, X3},P3 = {X3, X5}
显然用最小径集比较各基本事件的结构重要顺序比用最小割集方便。
根据以上四条原则判断:X1,X3都各出现2次,且2次所在的最小径集中基 本事件个数相等,所以I"1)=I"3),X2, X4,X5都各出现1次,但X2所在的最 小径集中基本事件个数比X4,X5所在最小径集的基本事件个数多,故Iφ(4)= Iφ (5)>Iφ(2)'由此得各基本事件的结构重要顺序为:
Iφ(1) =Iφ(3)>Iφ(4)=Iφ(5)>Iφ(2)
在这个例子中,近似判断法与精确计算各基本事件结构重要系数方法的结果 是相同的。分析结果说明:仅从事故树结构来看,基本事件X1和X3对顶上事件 发生影响最大,其次是X4和X5, X2对顶上事件影响最小。据此,在制定系统防 灾对策时,首先要控制住X1和X3这两个危险因素,其次是X4和X5,对X2要根 据情况而定。
基本事件的结构重要顺序排出后,也可以作为制定安全检查表,找出日常管 理和重点控制的依据。
1)概率重要度分析。这是考察各基本事件发生概率的变化对顶上事件发生 概率的影响程度。顶上事件发生概率是一个多重线性函数g,对自变量Qi求一次 偏导,即可得该基本事件的概率重要系Ig(i),即
据此,可知每一基本事件如降低其发生概率,可以有效地降低顶上事件的发 生概率。若所有的基本事件的发生概率都等于1/2时,概率重要系数等于结构重 要系数。因此对较容易定量计算的事故树,应用此法可以准确求出结构重要系数。
2)临界重要度分析。一般,概率大的基本事件的概率减小比概率小的基本 事件的概率减小要容易,而概率重要系数并未反映此特性。
临界重要系数CIg⑺是从敏感度及自身发生概率的双重角度来考察各基本 事件的重要度标准,是从本质上反映事故树中各基本事件的重要程度,因此也就 更为科学、合理。
临界重要度的定义为
CIg (Z)= dng d In qt
由偏导数公式变换得
CIg (Z)= %顷
3)事故树的定量分析
进行事故树的定量分析,需要求出各基本事件发生的概率,可利用最小割集 和最小径计算顶上事件的发生概率。根据所得结果与预定的目标值进行比较,如 超出目标值,就应采取相应的安全对策措施,使顶上事件发生概率降至目标值以 下;如果顶上事件的发生概率及其造成的损失为可接受范围,则暂不考虑投入更 多的人力、物力。
…
FTA的应用范围比较广泛,非常适合于重复性较大的系统。
FTA的优点是如下:
1) 能识别导致事故的基本事件(基本的设备故障)与人为失误的组合,可 为人们提供设法避免或减少导致事故基本原因的线索,从而降低事故发生的可能 性;
2) 对导致灾害事故的各种因素及逻辑关系能作出全面、简洁和形象描述;
3) 便于查明系统内固有的各种危险因素,为设计、施工和管理提供科学依 据;
4) 使有关人员、作业人员全面了解和掌握各项防灾要点;
5) 便于进行逻辑运算,进行定性、定量分析和系统评价。
FTA的缺点是分析步骤多,计算复杂,且国内相关数据积累较少,进行定量 分析需要工作量大。
下面以燃爆事故为例,进行事故树分析。
1)燃爆事故树
]
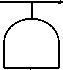
一氯甲烷、异丙醇均属甲类易燃易爆物质,在储存和反应过程中有发生燃烧 爆炸的可能性。燃爆事故树见图
一氯甲烷、异丙醇储运或反应设备
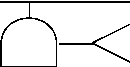
达爆炸极限

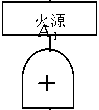
达可燃浓度
|
I I |
撞击火花 |
《 |
雷击火花 |
泄漏 |
通风不良 |
B5
B4
B6 B7
B3
电火花
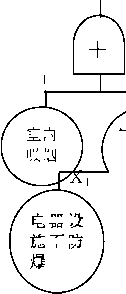
室内
吸烟
电器设
施不防
爆
防爆电 器损坏
危险区 内动火
B2
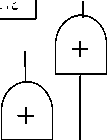
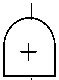
■2
|
} 储罐、 反应器 静电放 |
C1 |
人体 地电 |
X4
储桶
撞击
|
用铁制) |
/穿有铁 |
|
工具作 |
钉的鞋 |
|
业 |
工作 |
接地不良
静电积累
流速
过高
管道内 壁粗糙
未设防 静电接 地
接地电
阻不符 要求
X12
X13
C3避雷
失效
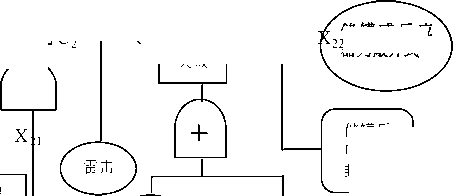
储罐反
应器密 封不良
未装避、
雷设施)D避雷器故障
储罐或反应 器为敞开式
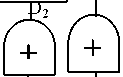
液体冲击
金属容器

飞溅液 体与空 气摩擦
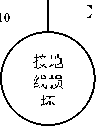
接地
线损
坏
X11
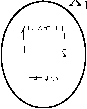
化纤品 与人体 摩擦
X15
X16
X14
设计 缺陷
作业中 与导体 接近
X24
图1-10燃爆事故树分析
避雷设 施损坏
防雷接 地电阻 超标
X19 X20
无排风 设施
X25
排风设 备损坏
未定时 或及时
X26
2)事故树定性分析
(1)求最小割(径)集
根据事故树最小割(径)集最多个数的判别方法判断,图所示事故树最小割 集最多有144个,最小径集11个,所以从最小径集入手分析较为方便。
该事故树的成功树结构函数为
T =A1 +A2 +X27
—口 '口 '口 '口 '口 '丄口 '丄口 '丄 Y ‘
=D 1B2B3B4B5 +B 6 +B 7 +X27
=X1 X2 X3 X4 X5 χ6χ7C1 C2 (x21 +C3 )+χ22 x23 +x24 X25 X26 +X27
【
-Y V 'γ 'γ 'γ 'γ 'γ 7n *n 'vy *γ 'vy '+y 'n '、+y * ‘
=X1 X2 X3 X4 X5 X6 X7 (D1 +D2 )(X15 +X16 )(X21 +X17D3 ) +X22 X23
+X24 X25 X26 +X27
=χ1χ2χ3χ4χ5χ6χ7 χ8χ9χ10χ11χ15χ17χ18 X19 X20
-k Y 'Y 'Y 'Y 'Y 'Y 'Y 'Y F F 'γ 'γ ‘
+ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X15 X21
+ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X16 X17 X18 X19 X20
+ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X16 X21
+ X1 X2 X3 X4 X5 X6 X7 X12 X13 X14 X15 X17 X18 X19 X20
''''''' ' ' ' ' '
+ X1 X2 X3 X4 X5 X6 X7 X12 X13 X14 X15 X21
+ X1 X2 X3 X4 X5 X6X7 χ12χ13χ14χ16χ17χ18 X19 X20
+ X1 X2 X3 X4X5 X6X7X12X13 X14 X16 X21
+ X22 X23 +X24 X25 X26 +X27
从而得出11个最小径集:
P1= {χ1, χ2, χ3, χ4, χ5, χ6, χ7, X8, X9, X10, X11, X15, X17, X18, X19,
P2= {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X15,
P3= {X1, χ2, χ3, χ4, χ5, χ6, χ7, X8, X9, X10, X11, X16, X17, X18, X19,
P4= {X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X16,
P5= {X1, χ2, χ3, χ4, χ5, χ6, χ7, X12, X13, X14, X15, X17, X18, X19,
P6= {X1, X2, X3, X4, X5, X6, X7, X12, X13, X14, X15,
P7= {X1, χ2, χ3, χ4, χ5, χ6, χ7, X12, X13, X14, X16, X17, X18, X19,
P8= {X1, X2, X3, X4, X5, X6, X7, X12, X13, X14, X16,
<
P9= {X22, X23}
p10= {χ24, χ25, X26}
P11= {X27}
(2)结构重要度分析
因为X27是单事件最小径集,所以Iφ(27)最大;X22, X23同在一个最小径 集中;X24, X25, X26同在一个最小径集中;X1, X2, 乂3, 乂4, 乂5, 乂6, 乂7同在8个最
小径集中;X8, X9, X10, X11同在4个最小径集中;X12, X13, X14同在4个最小径 集中;X17, X18, X19, X20同在4个最小径集中。
根据判别结构重要度近似方法,得到:
Iφ(1)= Iφ(2)= Iφ(3)= Iφ(4)= Iφ(5)= Iφ(6)= Iφ(7)
Iφ(8)= Iφ(9)= Iφ(10)=Iφ(11)
Iφ(12)= Iφ(13)= Iφ(14)
Iφ(17)= Iφ(18)= Iφ(19)=Iφ(20)
@
Iφ(22)= Iφ(23)
Iφ(24)= Iφ(25)=Iφ(26)
而X15, X16, X21与其他事件无同属关系。因此,只要判定Iφ(1),Iφ(3),Iφ (12),Iφ(15),Iφ(16),Iφ(17),Iφ(21),Iφ(22),Iφ(24)大小即可。
根据结构重要系数计算公式得到:
222
1 _ 27 _ 13.5
+ 212-1 = 215 =亍
()=216-1 + 215-1 + 213-1
1 (12) = 215-1+ 212-1 =酉
I(15) = I、] H--ττ-j- H
135
I (16) = I (15) = V
I (17) =+=
i (21)=尹1 +厂=戸
i (22)=剥=2
I (24)
11 --=— 23-1 4
1 (27) = 2-1 = 1
因此,得到结构重要顺序为:
Iφ (27) > Iφ (22) = Iφ (23) > Iφ (24) =Iφ (25) = Iφ (26)
>Iφ (1) =Iφ (2) =Iφ (3) =Iφ (4) =Iφ (5) = Iφ (6) =Iφ (7)
>Iφ (21) >Iφ (12) = Iφ (13) =Iφ (14) >Iφ (15) =Iφ (16)
>Iφ (8) =Iφ (9) =Iφ (10) = Iφ (11) >Iφ (17) =Iφ (18) =Iφ (19) = I
φ (20)
3)结论
〜
从燃爆事故树分析可知,火源与达到爆炸极限的混合气体构成了燃爆事故发 生的要素。基本事件X27 (达到爆炸极限)是单一事件的最小径集,其结构重要 系数最大,是燃爆事故发生的最重要条件。这就要求我们采取针对措施,如:用 气体报警器对混合气的浓度进行监视,一旦接近危险极限立即报警,使管理人员 立刻采取预防措施;加强通风排气降低混合气浓度和容器温度等。其次,最小径 集P9只由X22,X23组成,其重要度仅次于X27,由此可知容器的密封在防止燃 爆中具有重要地位。
事件树分析法
事件树分析法概述
事件树分析(EVent Tree Analysis,缩写ETA )是一种从原因推论结果的 (归纳的)系统安全分析方法,它按事故发展的时间顺序由初始事件出发,按每 一事件的后继事件只能取完全对立的两种状态(成功或失败、正常或故障、安全 或事故等)之一的原则,逐步向事故方面发展,直至分析出可能发生的事故或故 障为止,从而展示事故或故障发生的原因和条件。通过事件树分析,可以看出系 统的变化过程,从而查明系统可能发生的事故和找出预防事故发生的途径。事件 树分析适用于多种环节事件或多重保护系统的危险性分析,既可用于定性分析, 也可用于定量分析。它最初用于核电站的安全分析,在其他工业领域也得到广泛 的应用。
分析步骤
1) 确定初始事件
初始事件可以是系统或设备的故障、人员的失误或工艺参数偏移等可能导致 事故发生的事件.确定初始事件一般依靠分析人员的经验和有关运行、故障、事 故统计资料来确定;对于新开发系统或复杂系统,往往先应用其他分析、评价方 法分析的因素中选定(如用事故树分析重大事故原因,从其中间事件、基本事件 中选择),用事件树分析方法做进一步的重点分析。
2) 判定安全功能
系统中包含许多能消除、预防、减弱初始事件影响的安全功能(安全装置、 操作人员的操作等)。常见的安全功能有自动控制装置、报警系统、安全装置、 屏蔽装置和操作人员采取措施等。
》
3) 发展事件树和简化事件树
从初始事件开始,自左至右发展事件树。首先把初始事件一旦发生时起作用 的安全功能状态画在上面的分支,不能发挥安全功能的状态画在下面的分支。然 后依次考虑每种安全功能分支的两种状态,把发挥功能(正常或成功)的状态画 在次级分支的上面分支,把不能发挥功能(故障或失败)的状态画在次级分支的 下面分支,层层分解直至系统发生事故或故障为止.简化事件树是在发展事件树 的过程中,将与初始事件、事故无关的安全功能和安全功能不协调、矛盾的情况 省略、删除,达到简化分析的目的。
4) 分析事件树
(1) 找出事故连锁和最小割集
事件树各分支代表初始事件一旦发生后其可能的发展途径,其中导致系统事 故的途径即为事故连锁。一般导致系统事故的途径有很多,即有很多事故连锁。
事故连锁中包含的初始事件和安全功能故障的后继事件构成了事件树的最 小割集(导致事故发生的事件的最小集合)。事故树中包含多少事故连锁,就有 多少最小割集;最小割集越多,系统越不安全。
(2) 找出预防事故的途径
事件树中最终达到安全的途径指导我们如何采取措施预防事故发生。在达到 安全的途径中,安全功能发挥作用的事件构成事件树的最小径集(保证事故不发 生的事件的最小集合)一般事件树中包含多个最小径集,即可以通过若干途径防 止事故发生。
由于事件树表现了事件间的时间顺序,所以应尽可能地从最先发挥作用的安 全功能着手。
5) 事件树的定量分析
由各事件发生的概率计算系统事故或故障发生的概率。
当各事件之间相互统计不独立时,定量分析非常复杂;现仅就各事件之间相 互统计独立时的定量分析做简要的介绍。
(1)各发展途径的概率
各发展途径的概率等于自初始事件开始的各事件发生概率的乘积;
例如,图4-11所示事件树中各发展途径的概率计算如下:
初始事件
安全功能1
安全功能2
安全功能3
结果
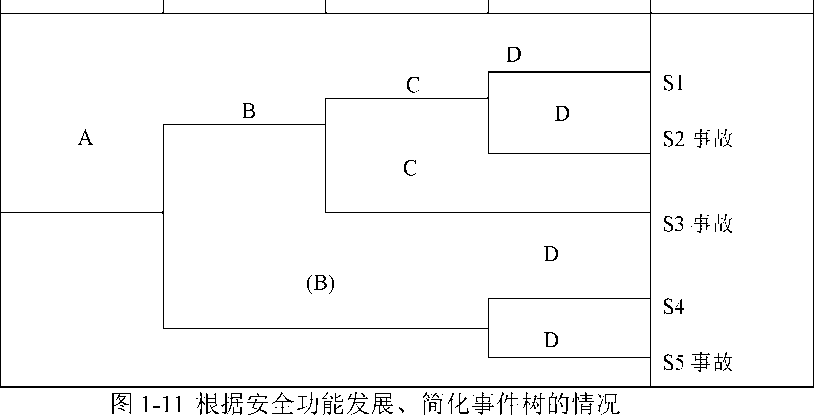
P [S1] =P[A] ∙ P [B] ∙ P [C] ∙ P [D]
P [S2] =P[A] ∙ P [B] ∙ P [C] ∙ P [D]
P [S3] =P[A] ∙ P [B] ∙ P [C]
P [S4] =P[A] ∙ P [B] ∙ P [D]
P [S5] =P[A] ∙ P [B] ∙ P [D]
(2)事故发生概率
事件树定量分析中,事故发生概率等于导致事故的各发展途径的概率和。对 于图4-2的事件树,其事故发生概率为:
P = P[S2]+P[S3]+P[S5]
应用示例
露天矿断钩跑车事故的事件树分析。
某露天矿铁路运输过程中,一列上坡行驶的列车的尾车连接器钩舌断裂,造 成尾车沿坡道下滑;由于调车员没有及时采取制止车辆下滑的措施,车速不断增 加;当尾车滑行到135站时,该站运转员误将其放行到上线;尾车进入上线后 继续滑行,经过117站时,该站运转员惊惶失措,导致尾车与前方检修车相撞, 造成一起多人伤亡事故。
选择断钩跑车为初始事件,针对该初始事件有三种安全功能(调车员采取制 动措施、站运转员将尾车放行进入安全线、117站运转员将尾车放行进入安全 线)。由初始事件开始发展事件树,得出图1 — 12所示的事件树。
调车员采取制动措施
____________________________________________________S1___________
断钩跑车 135站运转措施正确
-------- -----------------------S2---------
调车员未采取措施 117站运转措施正确
____________________ _______S3---------
135站运转失误
M转失误
----S4事故——
图1 — 12露天矿断钩跑车事故的事件树